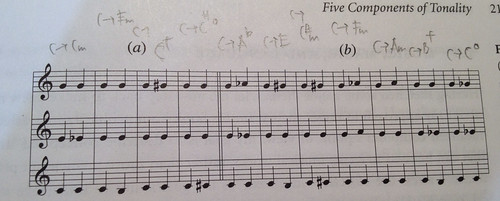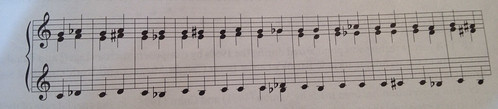この本は、調性とは一体何なのか、という音楽の根源的な問題に答えようとするのは、「やめて」、一般的に調性音楽といわれるクールな音楽に潜む法則を集めて使えるようにしよう、という至極プラグマティックな選択をする。音楽に潜む法則を五つ設定し、それについて精査していく。
その前に調性音楽とは何なのだろうか。ざっくり説明使用しよう。音楽をざっくり二つに分けるとすると、調性音楽と無調音楽に分けることができるが、調性音楽とは、簡単にいえば歌える音楽だ。歌えるというのは、記憶できるということだ。記憶できなければ、歌えない。なぜ調性音楽を記憶できるかというと、メロディの使用する音階が、ある程度固定されているためだ。音階が無限に使われる音楽は複雑すぎて、普通は歌えない。制限されていれば、覚えることが容易だ。
調性音楽は、メロディの選択肢が少ないため、記憶することができ、歌うことができる。対して無調の音楽は歌えない。
Lux aeterna
http://www.youtube.com/watch?v=OaC6Mqi-Pb4&feature=youtube_gdata_player
キューブリックが監督した2001年宇宙の旅で使用されたリゲティのこの楽曲は、合唱曲ではあるものの、普通は歌えないという意味では無調の音楽であるといえる。
いわゆる現代音楽だが、これを音楽だと認めてくれる心の広い人間はどうやら世界に一万人もいないらしい。現代音楽の巨匠の新作の売り上げ枚数がそれを下回るから、だそうだ。
このリゲティの楽曲がなぜ歌えないか?出てくる音階があまりに多すぎて、全然覚えれないからだ。だからこれは無調の音楽だ。
以上、これが私の考える調性音楽と無調の音楽だが、これに反論したい博学な方がいらっしゃると思う。確かに、この分類の仕方は雑だ!では、調性音楽とは何だろうか。説明できますか?実はかなり困難だと思う。というかできない。研究者の中でも議論が別れる。よくわからない、というか、定義が曖昧な用語なのだ。
そこで、彼は調性について説明しようとするのはやめにしよう、提案する。それよりも、クールな音楽に現れる技法を集めて使えるようにしようというのだ。
図1
図2
図3
彼の提案する技法の一部を紹介しよう。
図2はコードCmajorの構成音を、全音以内で動かしたら、どんな他のメジャーコードにも変化することを示している。
例えば一つ目の例は、CmajからDbmajに変化している。すべての声部を半音あげたので、どの声部も全音以内の移動である。以降すべての例は、Cmajの各声部が全音以内の移動をすることで、全てのメジャーコードに変化できることを示している。
つまり、我々はどんなメロディの動きにもフィットする和声をつけることができるということだ。これはかなり通常の和声感からすれば新しい。
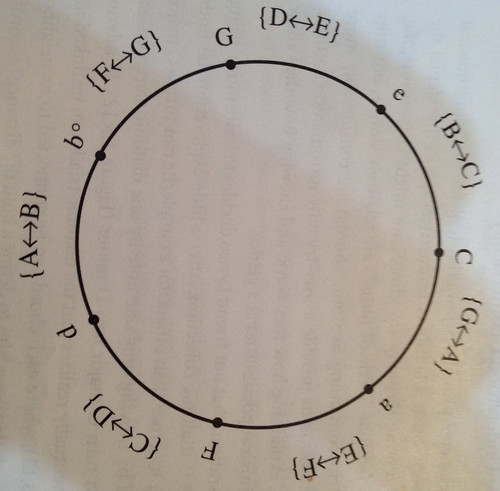
もう少しわかりやすい例を見てみよう。図3は、Cmajor scaleの中に含まれる音から和音を作る場合に、ある和音から一音だけ動かすと、他の和音に変化するが、その一音変えるだけで変化できる和音を隣りに並べた図だ。
大文字はメジャーコード、小文字はマイナーコード、○はディミニッシュコードだ。
例えばGmajとEminorは、一音だけ異なる。DをEに変えれば変化できる。だから円の中で隣り合っている。
この円はわかりやすいが、しかし大事なことを教えてくれる。つまり、我々が音楽の中で行っていることを図示することで、より簡単に把握することができるのだ。一番良くしられた音楽に関する図形はサイクルオブヒフスだ。
最後に図1は、もっとも抽象的な概念を示している。つまり、メジャーコードの声部のうち、二声部を半音動かすことによって、マイナーコードやディミニッシュコードや、オーギュメントコードなど、かなり多くのコードに変化できるが、この変化は声部の移動がとても少ないので、かなりスムーズだということを示している。
この三つのテクニックを使用すると、あるコードから他のあるコードへかなりスムーズに、しかしある種無限ともいえる選択肢に対して移動できる。おそらくは我々の感覚はこうしてモーダルな環境とコーダルな環境を行き来している。
以上第一章で扱われた内容のうち、わかりやすいテクニックを紹介して見た。翻訳は引き続き行って行きます。
興味がある方は是非応援のほど、よろしくお願い致します。